Huffman树的编码与译码
哈夫曼编码译码
先看题目:
首先这是一道PTA的题目,作为博主数据结构与算法这门课程的假期实践作业。
编写一个哈夫曼编码译码程序:
按词频从小到大的顺序给出各个字符(不超过30个)的词频,根据词频构造哈夫曼树,给出每个字符的哈夫曼编码,并对给出的语句进行译码。
为确保构建的哈夫曼树唯一,本题做如下限定:
(1)选择根结点权值最小的两棵二叉树时,选取权值较小者作为左子树。
(2)若多棵二叉树根结点权值相等,按先后次序分左右,先出现的作为左子树,后出现的作为右子树。
生成哈夫曼编码时,哈夫曼树左分支标记为0,右分支标记为1。
输入格式:
第一行输入字符个数n;第二行到第n行输入相应的字符及其词频(可以是整数,与可以是小数);
最后一行输入需进行译码的串。
输出格式:
首先按树的先序顺序输出所有字符的编码,每个编码占一行;最后一行输出需译码的原文,加上original:字样。
输出中均无空格
输入样例:
3
m1
n1
c2
10110
输出样例:
c:0
m:10
n:11
original:mnc
题目分析:
题目给出了n个字符以及他们的频率,也就是说给出了n个结点,让我们用这n个结点构建一个Huffman树,然后又给出一段哈夫曼编码,让我们在所构建的Huffman树的基础上,对该编码进行翻译。
所以这道题难点在于怎么构建这样一颗Huffman树(结点的选取、编码和译码)。
实验步骤:
根据Huffman树的性质我们可以知道,Huffman树中没有度为1得结点. 只有度为0和度为2得结点. 则一棵 有n个叶子结点得哈夫曼树共有2n-1个结点
所以题目给了n个结点(叶子结点),那么我们构建的Huffman树就会有2n-1个结点。
不妨画图看看?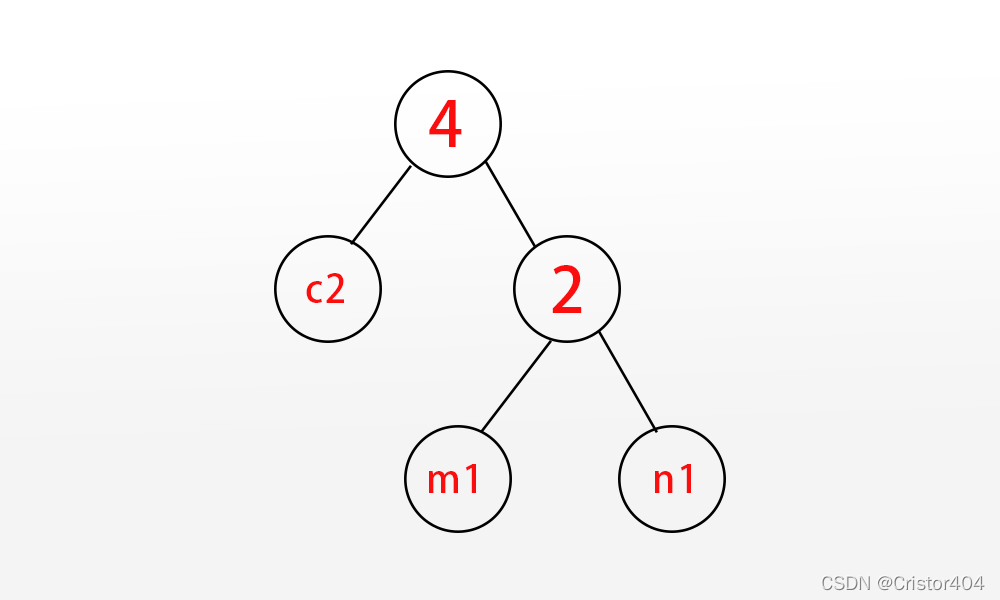
我们可以构建出这样一颗Huffman树,首先我们来创建一个树结点的结构体,每一个结点都存有: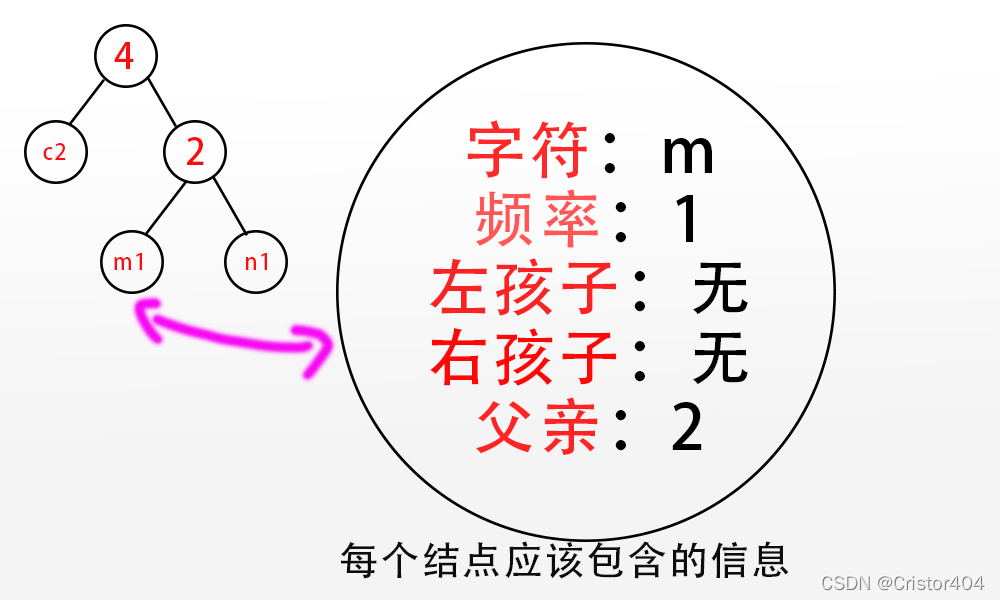
诶呀,图里忘记画 哈夫曼编码 这一项咯QWQ(也就是下图的char* code;)
↑对应的代码:
1 | //Huffman树结点结构体 |
然后,将这些结点组合起来,形成一颗树: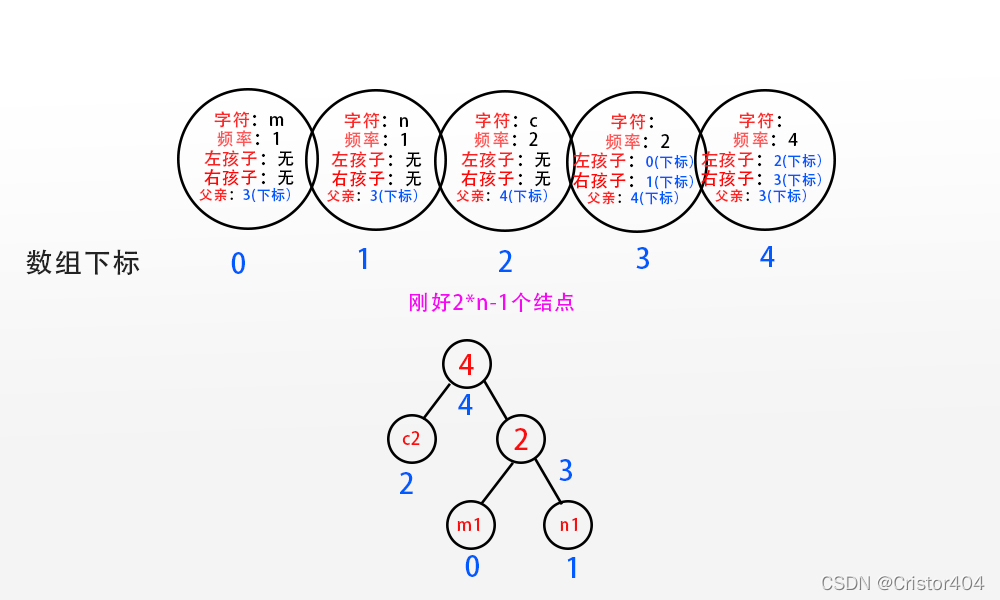
↑对应的代码:
1
2
3
4
5 //Huffman树结构体
typedef struct HFTree{
TreeNode* data;//用堆实现该Huffman树
int length;//该树总结点的个数
}HFTree;
好的,构建完树的结构体之后呢,我们可以先编写程序的输入(main)部分:
1 |
|
好的,这样我们就拿到的输入的数据,接下来我们需要对拿到的字符和频率(也就是结点)进行Huffman树的构造咯!
我们可以写一个初始化函数:
1 | //初始化哈夫曼树 |
初始化之后呢,树的状态就为下图所示咯:(只初始化给定的结点,之后的结点我们后续构造)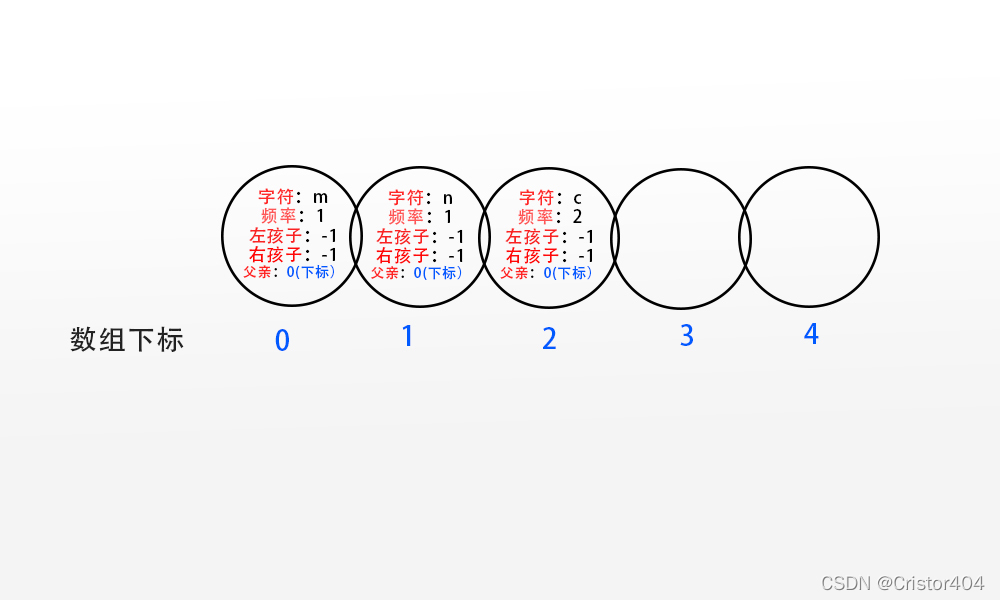
下面就是创建一个Huffmna树的函数咯,但是我们还需要做一些准备:
因为在创建一颗Huffman树时,需要从所有结点之中,选择两个权值最小的结点来进行组合,所以我们需要先编写一个选择最小两个结点的下标的函数:
1 | //选择两个权值最小的结点,每次都会返回两个最小的结点 |
有了这玩意之后,我们就可以很开心的来写一个构建Huffmna树的函数咯!(把给定的叶子结点进行结合,从下往上构建父结点)
1 | //创建Huffman树 |
这是结合完毕之后的树结构状态图: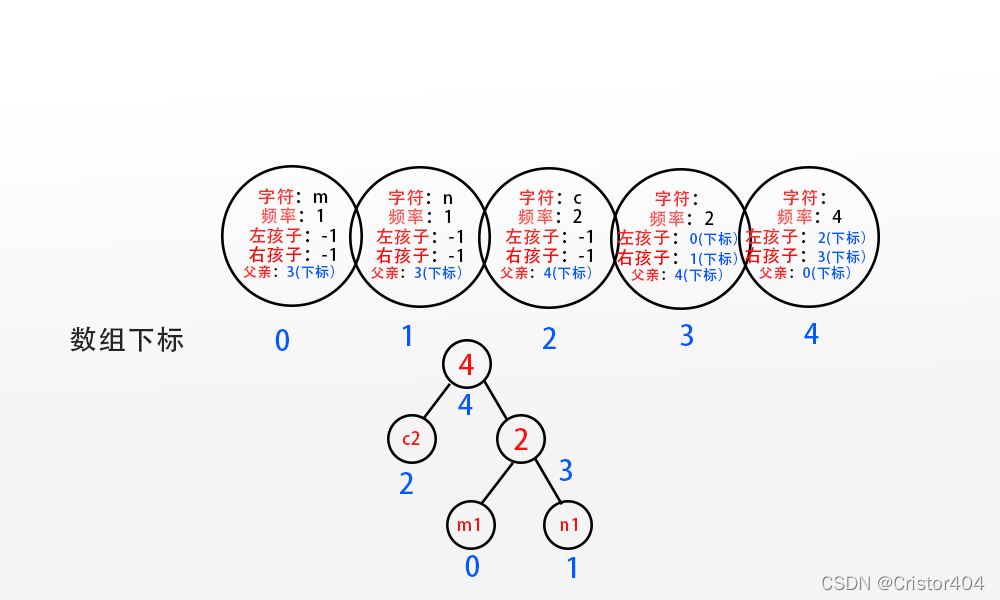
发现变化了嘛?
那么这个树的结构算是给我们给整出来了,但是每一个结点都还差自己的一个东西,那就是他们的Huffman编码!
根据题意:哈夫曼树左分支标记为0,右分支标记为1,那么3个叶子结点的Huffman编码就如下: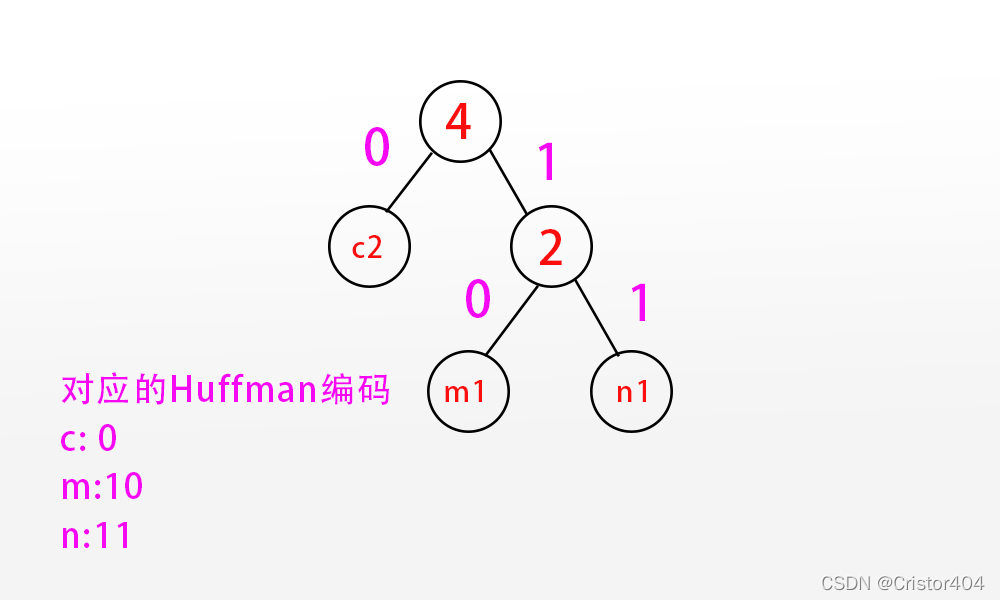
开始编写编码器:
基本思路:
我们可以从叶子节点开始回溯,创建一个字符串用来存Huffman编码,左孩子就接‘0’ 右孩子就接‘1’ 直到回溯到的结点的父亲为0时停止,拿m来举例:
最后得到的字符串为:01 这与我们的预期相反 所以我们要逆序将这个字符串加入到结点的哈夫曼编码项中,此时m这个叶子结点的code项就为:10 符合我们的预期!
1 | //Huffman编码器 |
这时,我们的Huffman树就算是正式构建完毕,所有的结点都有了参数咯,那么我们不妨将它遍历出来看看!
来写一个遍历函数吧:
1 | //递归遍历Huffman树 T->length-1为根结点 |
我们得到了这样的结果:

嗯嗯,很好,接下来最后一件事情就是给题目给出的这一段谜语来个翻译就欧克!
再来一个解码函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 //Huffman译码
char* Decode(char* str,int length,HFTree* T){
int index = length - 1,ct = 0,j = 0;
char ch;
ch = str[0];
char* res = (char*)malloc(sizeof(char)*MAX_INT);
while(true){
//当密文字符为0时向左走
if(ch == '0'){
index = T->data[index].lchild;
//为1时向右走
}else if(ch == '1'){
index = T->data[index].rchild;
}
//直到遍历到叶子节点
if(T->data[index].lchild == -1 || T->data[index].rchild == -1){
//此时的字符值即为这一段密文的密码字符
res[ct] = T->data[index].Ch;
ct++;
//回到根结点
index = length-1;
}
//记录当前遍历密文的位置
j++;
ch = str[j];
//当走完时直接及解码完成 退出循环
if(j == (int)strlen(str))
break;
}
return res;
}
ok大功告成,我们来看看结果吧!
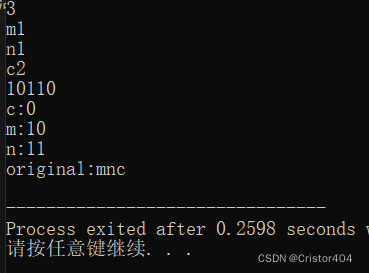
上PTA看看结果捏:
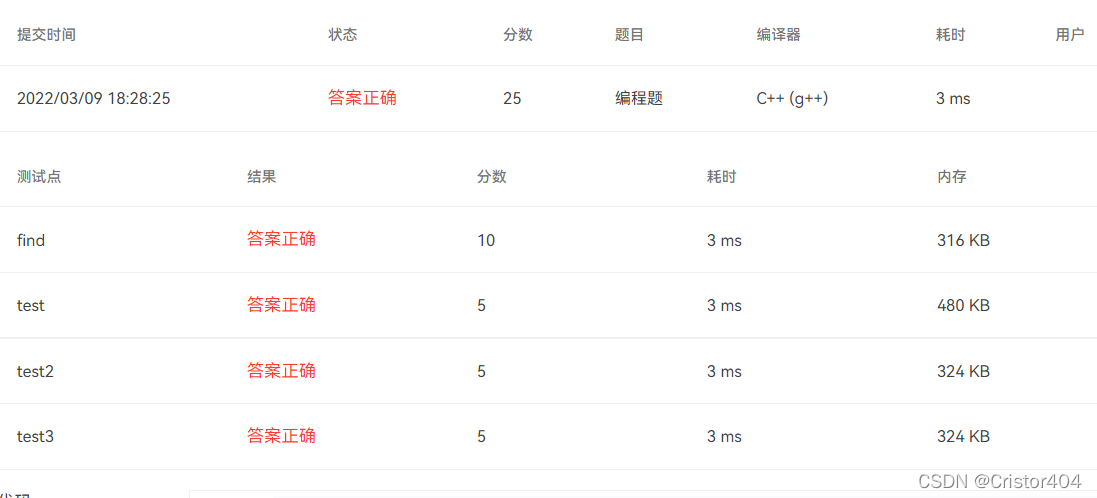
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
using namespace std;
//Huffman树结点结构体
typedef struct TreeNode{
double weight;//因为频率有可能为小数,所以用double
char Ch;//用于存放该节点字符
char *code;//用于存放该字符的 Huffman编码
int parent,lchild,rchild;//存放每个结点的 父节点 以及 子结点
}TreeNode;
//Huffman树结构体
typedef struct HFTree{
TreeNode* data;//用堆实现该Huffman树
int length;//该树总结点的个数
}HFTree;
//初始化哈夫曼树
HFTree* initTree(double* weight,char* ch,int n){
HFTree* T = (HFTree*)malloc(sizeof(HFTree));
//根据性质,n个结点生成的Huffman树会有2*n-1个结点
T->data = (TreeNode*)malloc(sizeof(TreeNode)*(2*n-1));
T->length = n;
//初始化每个结点
for(int i = 0; i < n; ++i){
T->data[i].Ch = ch[i];
T->data[i].weight = weight[i];
T->data[i].parent = 0;
T->data[i].lchild = -1;
T->data[i].rchild = -1;
//初始化每个结点的code数组
T->data[i].code = (char*)malloc(sizeof(char)*MAX_INT);
memset(T->data[i].code,'\0',MAX_INT);
}
return T;
}
//选择两个权值最小的结点
int* selectMin(HFTree* T){
//定义两个哨兵变量,他们的值为double所表示的最大值
//(numeric_limits<double>::max)();
double min = MAX_Double;
double secondMin = MAX_Double;
//两个最小结点的下标
int minIndex;
int secondIndex;
//先选择第一小的结点
for(int i=0;i<T->length;++i){
//只要没有父节点就可以选择
if(T->data[i].parent == 0){
if(T->data[i].weight < min){
min = T->data[i].weight;
minIndex = i;
}
}
}
//其次选择第二小的结点
for(int i =0;i<T->length;++i){
//没有父节点且不等于第一小的才选择
if(T->data[i].parent == 0 && i != minIndex){
if(T->data[i].weight < secondMin){
secondMin = T->data[i].weight;
secondIndex = i;
}
}
}
//因为返回两个值,所以可以使用指针
int* res = (int*)malloc(sizeof(int)*2);
res[0] = minIndex;
res[1] = secondIndex;
return res;
}
//Huffman编码器
void Hfmcode(HFTree* T,int n){
//分别给n个字符编码
for(int k=0;k<n;k++){
//从0号位的叶子节点开始回溯
int i = 0,j = 0;
int ch = k;
//记录单个字符的编码
char str[MAX_INT];
memset(str,'\0',MAX_INT);
int parent = T->data[k].parent;
for(i = n-1;parent != 0;i--){
//如果该左孩子与 回溯起点index相符
if(T->data[parent].lchild == ch){
str[j++] = '0';
ch = parent;
//向上回溯
parent = T->data[ch].parent;
}else{
//同上 右孩子.....
str[j++] = '1';
ch = parent;
parent = T->data[ch].parent;
}
}
int f = 0;
//因为是回溯编码,所以需要反转
for(int s = j-1;s>=0;s--){
T->data[k].code[f] = str[s];
f++;
}
}
}
//创建Huffman树
void createHFTree(HFTree* T,int nn){
int* res;
int min;
int secondMin;
int n = T->length * 2 - 1;
for(int i = T->length; i < n;++i){
T->data[i].parent = 0;
res = selectMin(T);
min = res[0];
secondMin = res[1];
//给父节点赋值
T->data[i].weight = T->data[min].weight + T->data[secondMin].weight;
T->data[i].lchild = min;
T->data[i].rchild = secondMin;
//给儿子们赋值
T->data[min].parent = i;
T->data[secondMin].parent = i;
T->length++;
}
//为每个字符编码
Hfmcode(T,nn);
}
//递归遍历Huffman树 T->length-1为根结点
void preOrder(HFTree* T,int index){
if(index != -1){
if(T->data[index].lchild == -1 || T->data[index].rchild == -1)
cout << T->data[index].Ch <<":"<<T->data[index].code<<endl;
preOrder(T,T->data[index].lchild);
preOrder(T,T->data[index].rchild);
}
}
//Huffman译码
char* Decode(char* str,int length,HFTree* T){
int index = length - 1,ct = 0,j = 0;
char ch;
ch = str[0];
char* res = (char*)malloc(sizeof(char)*MAX_INT);
while(true){
//当密文字符为0时向左走
if(ch == '0'){
index = T->data[index].lchild;
//为1时向右走
}else if(ch == '1'){
index = T->data[index].rchild;
}
//直到遍历到叶子节点
if(T->data[index].lchild == -1 || T->data[index].rchild == -1){
//此时的字符值即为这一段密文的密码字符
res[ct] = T->data[index].Ch;
ct++;
//回到根结点
index = length-1;
}
//记录当前遍历密文的位置
j++;
ch = str[j];
//当走完时直接及解码完成 退出循环
if(j == (int)strlen(str))
break;
}
return res;
}
int main(){
//输入n个字符
int n;
scanf("%d",&n);
getchar();
//初始化n个 char和double类型的数组 用于存放 字符和对应的频率
char* chNums = (char*)malloc(sizeof(char)*n);
double* nuNums = (double*)malloc(sizeof(double)*n);
//输入 字符以及相应的频率
for(int i=0;i<n;++i){
scanf("%c%lf",&chNums[i],&nuNums[i]);
getchar();
}
//输入 需要译码的字符串
char str[MAX_INT];
scanf("%s",str);
getchar();
//创建一棵Huffman树
HFTree* T = initTree(nuNums,chNums,n);
createHFTree(T,n);
//遍历每个字符及其编码
preOrder(T,T->length-1);
//遍历解码后的密文
cout<<"original:"<<Decode(str,T->length,T)<<endl;
return 0;
}
博主的编程水平比较菜,写这一题花了挺长时间的,主要卡在了给每个字符编码,但是在写完了编码函数提交之后,第一个测试点不通过,以为是自己的思路有问题,而且PTA也不给测试点的数据,搞得不知道哪里出问题了,改了好几天,最后发现,原来是在判断最小的两个结点时,哨兵的值设置的太小,然后测试点给了一个很大的频率,导致一直没过,也是随便改改提交突然全过了,算是乱碰给碰出来了hhh,发出来给大家借鉴一下,如果你有更好的想法的画,欢迎与博主进行讨论交流!

