Cristor计算机系统的笔记
《计算机系统基础知识》 の笔记
计算机的基本硬件系统组成
运算器 控制器 存储器 输入设备 输出设备 等
其中
运算器+控制器 = CPU
这些两个部件被集成在一起称为中央处理单元
CPU:
运算器+控制器 = CPU
运算器:
主要做运算:所有的 与或非(逻辑) 加减乘除 附加(算数)….. 以及加工数据
运算器包括的部件有:
算术逻辑单元(ALU):
是运算器的重要组成部件,负责处理数据(算数运算,逻辑运算)累加寄存器(AC):
是一个通用寄存器(暂时存数据用的),它为ALU服务,当AUL执行算数或者逻辑运算时,他提供一个工作区。(比如ALU需要做一个减法 从内存中读取被减数到AC,然后再取减数到AC,然后结果也存AC里面,也就是说 一个ALU必须要有1个或者1个以上AC。)数据缓冲寄存器(DR):
作为CPU和内存、外部设备之间的数据传送的中转站;因为CPU和内存处理数据的速度不一致,所以需要DR来进行缓冲。个人理解为缓存。状态条件寄存器(PSW):
执行完算数指令之后,建立一个条件码的内容,比如1-1=0;它就会给一个运算结果为0的标志…(不太了解)
控制器:
主要用于 产生指令的操作信号 并且将这个信号送往相应的部件进行处理 控制指令执行顺序….
运算器只能完成运算,但是控制器却能控制整个CPU的工作,它决定了CPU执行过程的自动化。
它的任务:1.保证程序正确执行 2.处理异常事件
这里引入一个概念:
指令 = 操作码 + 地址码
它包括的部件有:
指令寄存器(IR):
CPU执行指令时,从内存中取数据存入DR(运算器中的DR)中,然后再送入IR暂存,指令译码器(ID)再对IR内的内容产生各种微操作指令,控制其他组成的部件工作,完成所需的功能。
个人理解为 暂存一下指令 的一个元器件
而且操作码和地址码都要存在IR里面
且用户无法直接访问IR内的数据☆☆程序计数器(PC):
PC可以寄存信息和计数(两种功能)
程序的执行分两种情况,一是顺序执行, 二是转移执行。在程序开始执行前,将程序的起始地址送入PC,该地址在程序加载到内存时确定,因此PC的内容即是程序第一条指令的地址。执行指令时,CPU自动修改PC的内容,以使使其保持的总是将要执行的下一条指令的地址。 由于大多数指令都是按顺序来执行的,所以修改的过程通常只是简单地对PC加1.当遇到转移指令时,后继指令的地址根据当前指令的地址加上一个向前或向后转移的位移量得到,或者根据转移指令给出的直接转移的地址得到。可以简单理解为:PC+1就可以让CPU执行下一条指令
地址寄存器(AR):
保存当前CPU当前所访问的内存单元的地址。指令译码器(ID):
我们刚才提到,指令 = 操作码+地址码,而ID只对操作码进行分析,识别指令规定的操作,然后向操作控制器发出具体的控制信号,从而控制各个部件工作,完成所需的功能。
基本单位和进制转换:
基本单位和进制转换:
基本单位:
从小到大↓
位(比特) b bit
字节 B byte 1B=8b
千字节 KB 1KB = 1024B = 210 B
兆字节 MB 1MB = 1024KB = 210 KB
吉字节 GB 1GB = 1024MB = 210MB
太字节 TB 1TB = 1024GB = 210GB
最小的数据单位:bit
最小的存储单位:byte
常见的几种进制:
十进制(D) 0
91
二进制(B) 0
八进制(O) 07F
十六进制(H) 0
进制转换
按权展开求和:
把 n进制 转化成对应的 10进制
十进制转十进制:
173(D) = 1X100 + 7X10 + 3X1
= 1X102 + 7X101+3X100 = 173(D)
同理我们也可以得到
二进制转十进制:
1001001(B) →
1X26+0X25+0X24+1X23+0X22+0X21+1X20 = 73(D)
短除法
八进制转十进制:
255(O) → 2X82 + 5X81 + 5X80 = 173(D)
十六进制转十进制:
首先我们来看看十六进制的数从0到15是怎么表示的:
0 1 2 3 4 5 6 7 8 9 A B C D E F
AD(H) = Ax161 + Dx160 = 173(D)
十进制转二进制原理(短除法):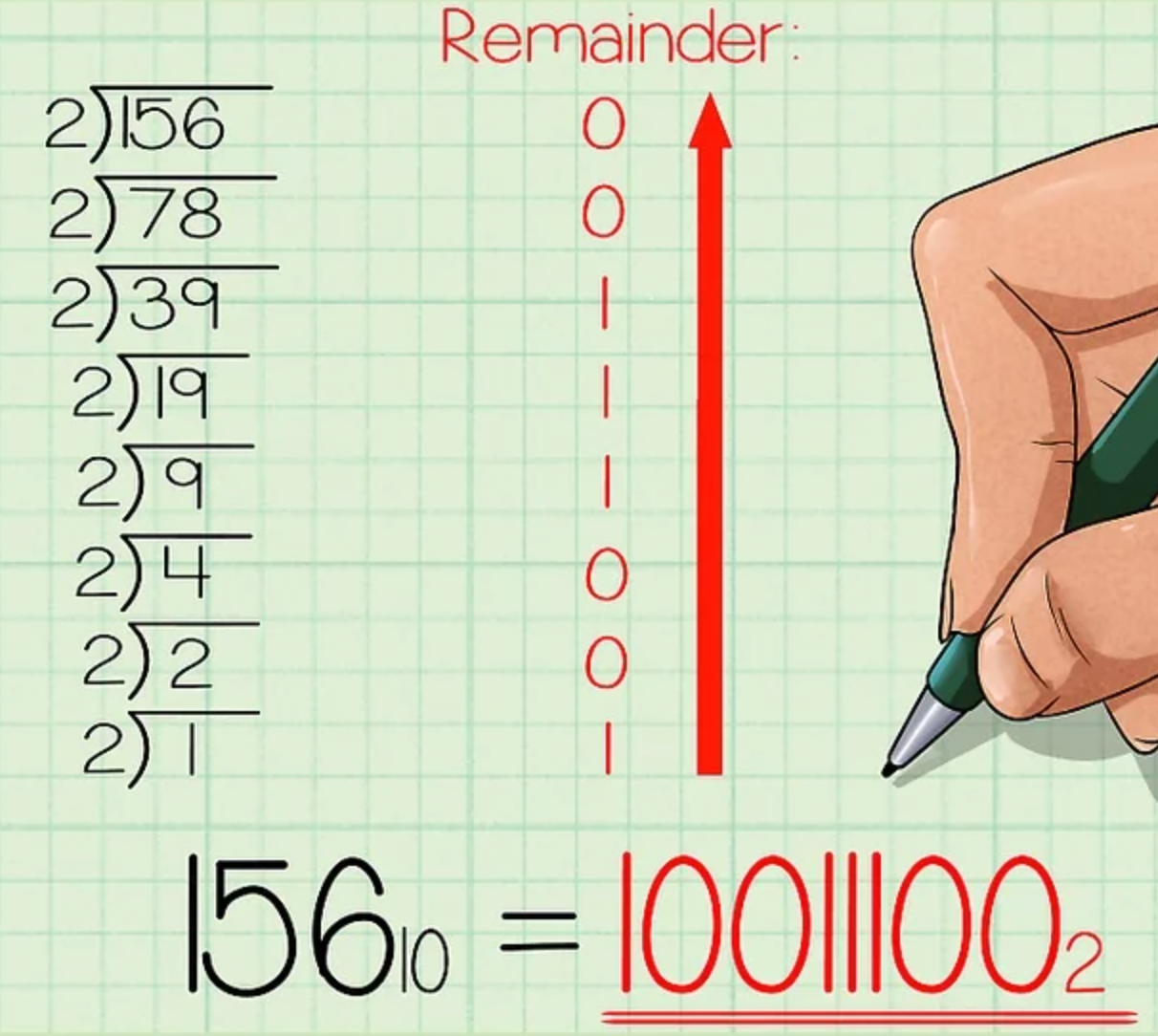
↑如图所示,依次除2,把余数倒着写,即可
八进制转十进制或者十六进制转十进制方法类似,都可以使用短除法来计算。
PS:
三位二进制数 对应 一位八进制数
四位二进制数 对应 一位十六进制数
进制的加减法
原理:逢n进1
例如10进制:
193 3+9 = 12 我们把12-10 = 2 进一
+89 十位就是 9+8+1 = 18 我们把 18 -10 = 8 进一
——
282 百位就是 1+1 = 2
同理,十六进制也一样:
ABDFE E+4 = 18 我们把18-16 = 2 所以该位是2 向高位进1
+1024 F+2+1 = 18 我们把 18 - 16 = 2 所以该位是2 向高位进1
D+0+1= 13 没有超过16 所以该位是 E
B+1 = C 没有超过16 所以该位是 D
A无数可加 所以该位还是 A
_ _
得到 ACE22
进制的减法
原理:借1当n
例如十进制减法:
27 我们发现7-9不够于是向高位借1
-9 所以高位减1 低位+10(也就是对应的进制n) 得到17-9=8
__
18
同理,二进制也一样:
100(D)
- 1 我们看见低位0-1不够,于是我们向第二个兄弟借1,发现第二个兄弟也是0,于是再向左边的第一个兄弟借1
所以此时第一个兄弟减1 变成0 此时:020
因为第二个兄弟向第一个兄弟借到了1 第三个兄弟还没有问第二个兄弟借到1
所以此时:012 所有的兄弟都借到了属于自己的数
这个时候就可以减1咯
最后得到:
100(D)
- 1(D)
_ _
011(D)
同理,十六进制和八进制也是同样的方法
数据的表示:
PS:
各种数值在计算机中表示的形式称为机器数,其特点是采用二进制计数制,数的符号用0和1表示,小数点则隐含,表示不占位置。机器数对应的实际数值称为数的真值。
机器数有无符号数和带符号数之分。无符号数表示正数,在机器数中没有符号位。对于无符号数,若约定小数点的位置在机器数的最低位之后,则是纯整数:若约定小数点的位置在机器数的最高位之前,则是纯小数。对于带符号数,机器数的最高位是表示正、负的符号位,其余位则表示数值。为了便于运算,带符号的机器数可采用原码、反码和补码等不同的编码方法,机器数的这些编码方法称为码制。
为了方便运算,带符号的机器数可以采用原码、反码和补码等不同的编码方法,机器数的这些编码方法称为码制
PS:正数的原码/反码/补码 完全相同 而负数的则不同
原码:
在原码表示法中,最高位是符号位 0表示正号,1表示负号,其余的n-1位表示数值的绝对值。数值0的原码表示有两种形式:
[+0]原=0 000000,[-0]原=1 0000000
[+1]原 = 0 0000001 [-1]原 = 1 0000001
[+127]原 = 0 1111111 [-127]原 = 1 1111111
[+45]原 = 0 0101101 [-45]原 = 1 0101101
由于第一位是符号位 所以我们还有7位可以使用
由于每一位对于着2的n次方
所以右到左分别是: 64 32 16 8 4 2 1
当我们需要用原码来表示一个数字时 我们可以从右到左找到第一个比它大的数
比如我们要找:45 我们可以从右到左 发现64比45大,于是我们不看64,直接看右边的32 16 8 4 2 1,想办法凑出45来
首先45-32 = 13 32这个位置标记1
然后13-16 不够减 所以16这个位置标记0
然后13-8 = 5 所以8这个位置标记1
然后5-4 = 1 所以4这个位置标记1
然后2-1 不够减 所以2这个位置标记0
然后1-1 = 0 所以1这个位置标记1
刚好凑出一个完整的45 然后前面的64的位 我们直接忽略了 所以我们要补一个0
最后我们可以凑出来一个[+45]原 = 0 0101101
非常简单
反码:
在反码表示中,最高位是符号位,0表示正号,1表示负号,正数的反码与原码相同,负数的反码则是其绝对值按位求反。数值0的反码表示有两种形式: [+0]反 = 0 0000000 [-0]反=1 1111111
原码转反码的方式:
除了符号位不变 其他的全部按位取反
例如:
[+1]原 = 0 0000001 [+1]反 = 0 1111110
[+45]原 = 0 0101101 [+45]反 = 0 1010010
[-127]原 = 1 1111111 [-127]反 = 1 0000000
补码:
在补码表示中,最高位为符号位,0表示正号,!表示负号,正数的补码与其原码和反码相同,负数的补码则等于其反码的末位加1.在补码表示中,0有唯一的编码: [+0]补 = 0 0000000
例如:
[-3]反1 1111100 [-3]反1 1111101
[-127]反 = 1 0000000 [-127]反 = 1 0000001